Greedy Algorithm

Posted on | In |
Words count in article: 908 | Reading time ≈ 3
贪心算法相关题解

[45] Jump Game II

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Your goal is to reach the last index in the minimum number of jumps.

贪心算法, 局部解得到最优解.

解题思路: 每次查找当前位置能够到达的位置中, 能跳到最远位置的位置A, 下次就跳到位置A, 然后再从位置A能到达的位置中, 再找能跳到最远位置的位置, 如此循环.

但是官方解答虽然简洁, 但是我不是看的很明白, 还是暂时先贴自己的直白解法吧.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
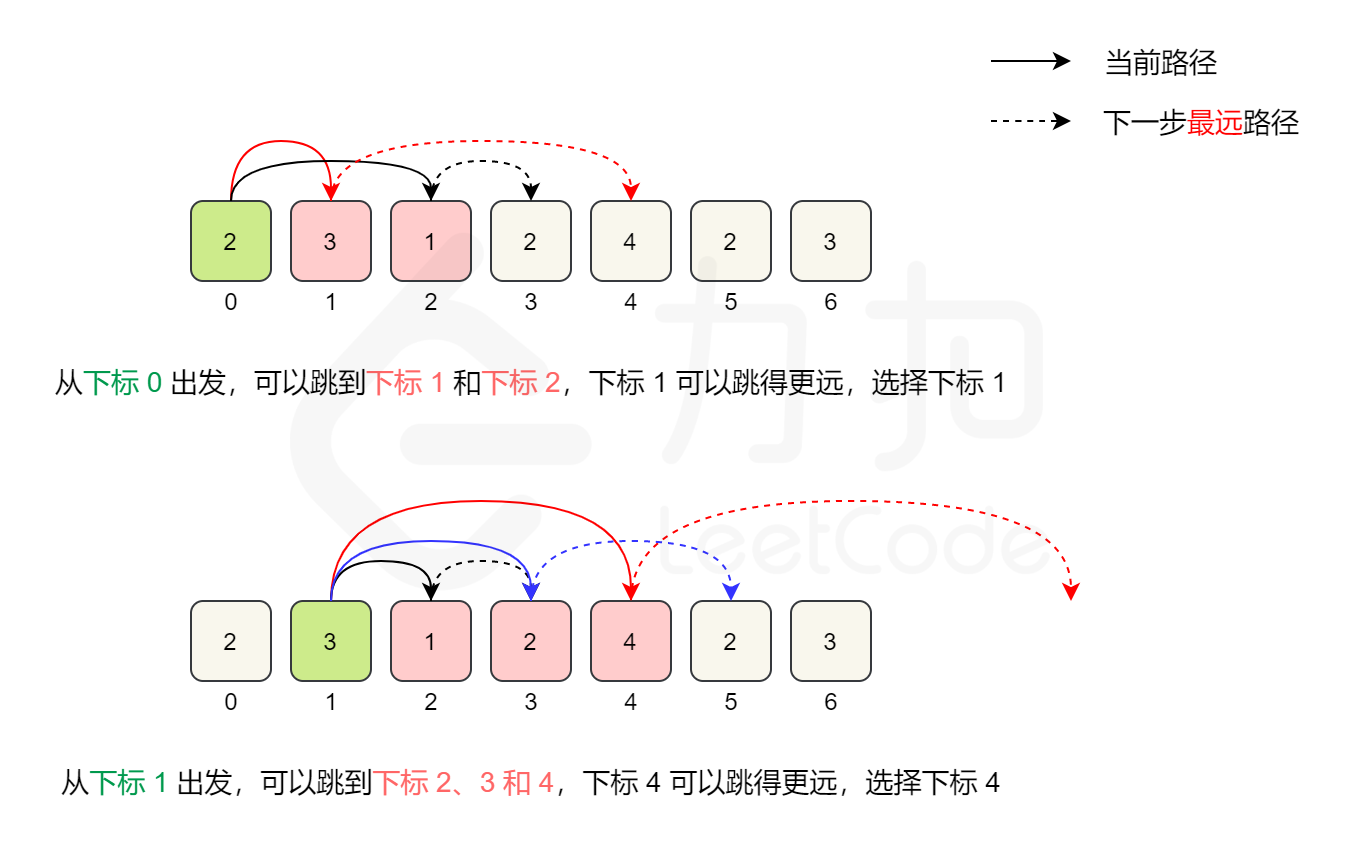
36
// 对于当前index, 每次在能跳到的范围内
// 跳到能跳到更远地方的index
var jump = function (nums) {
  let len = nums.length;
  if (len == 1)
    return 0;
  if (nums[0] >= len - 1)
    return 1

  let step = 0;
  let nextPosMap = { 'index': 0, 'maxIndex': 0 + nums[0] };

  for (let i = 0; i < len;) {
    let indexLimit = i + nums[i];
    // 在寻找下一步跳的位置时, 步数加一
    step++;
    for (let j = i + 1; j <= indexLimit && j < len; j++) {
      if (j + nums[j] > nextPosMap.maxIndex) {
        nextPosMap.index = j;
        nextPosMap.maxIndex = j + nums[j];
      }
    }
    // index != i, 说明能跳到更远距离的index更新了, 这时才需要将当前节点 i 移到index
    // 其实肯定更新, 题目已经说了能跳到最后
    // 移动才算跳了一步
    // 同时能跳到的最远位置不要超过数组边界
    // 超过数组边界则表示步数已经能计算出来了 return
    if (nextPosMap.maxIndex < len - 1) {
      i = nextPosMap.index;
    } else {
      // 当最大位置能到达最后时, 返回step+1
      // 把跳到最后位置的一步也加上
      return step + 1;
    }
  }
};

[55] Jump Game

Given an array of non-negative integers, you are initially positioned at the first index of the array.

Each element in the array represents your maximum jump length at that position.

Determine if you are able to reach the last index.

一开始尝试使用递归做法, 计算所有的可能性, 但是想也不是最好的解法, 最后很可能超时, 果不其然超时.

于是就去看网上解法, 这里的考点是贪心算法.

贪心算法（又称贪婪算法）是指，在对问题求解时，总是做出在当前看来是最好的选择。也就是说，不从整体最优上加以考虑，算法得到的是在某种意义上的局部最优解

该题的大概思路是:

数组的第一个元素的值为 reach, 从数组的第一个元素开始, 每次计算在reach范围内的元素们所能到达的最远距离, 是否超过reach, 如果超过了, 就更新reach值为较大值. 直至reach的值超过lastIndex 返回 true.

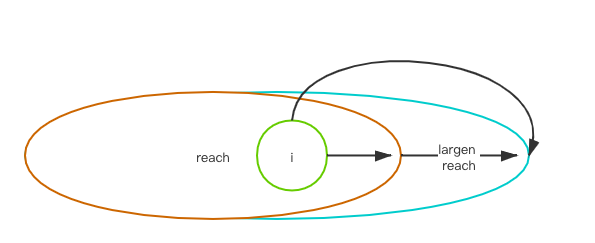
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
/**
 * @param {number[]} nums
 * @return {boolean}
 */
// 递归超时 使用贪心算法求解
// 局部能够到达的最大范围, 也是全局能够到达的最大范围
var canJump = function (nums) {
  let reach = nums[0];
  // 需要注意的点是,这里reach的值不一定就>1, 所以i不一定就从1开始
  // 还是从0开始能够包含所有情况, 这么写因为有个特例 [0]
  // 同时注意限制 i 的范围, i 是指 reach 能够到达的位置范围, 不能超过 reach
  for (let i = 0; i < nums.length && i <= reach; i++) {
    if (nums[i] + i > reach) {
      reach = nums[i] + i;
      // console.log(reach);
    }
    // 当能到达的范围超过数组的最后 index 时, 返回 true
    if (reach >= nums.length - 1)
      return true
  }
  // 能到达的元素位置都尝试了, 但是没有一个位置可以到达最后一个元素
  return false
};
0%